← Back to home

Physics-Constrained Flow Matching

NeurIPS 2025

Utkarsh *, Pengfei Cai *, Alan Edelman, Rafael Gómez-Bombarelli, Christopher Vincent Rackauckas
*Equal contribution

Massachusetts Institute of Technology

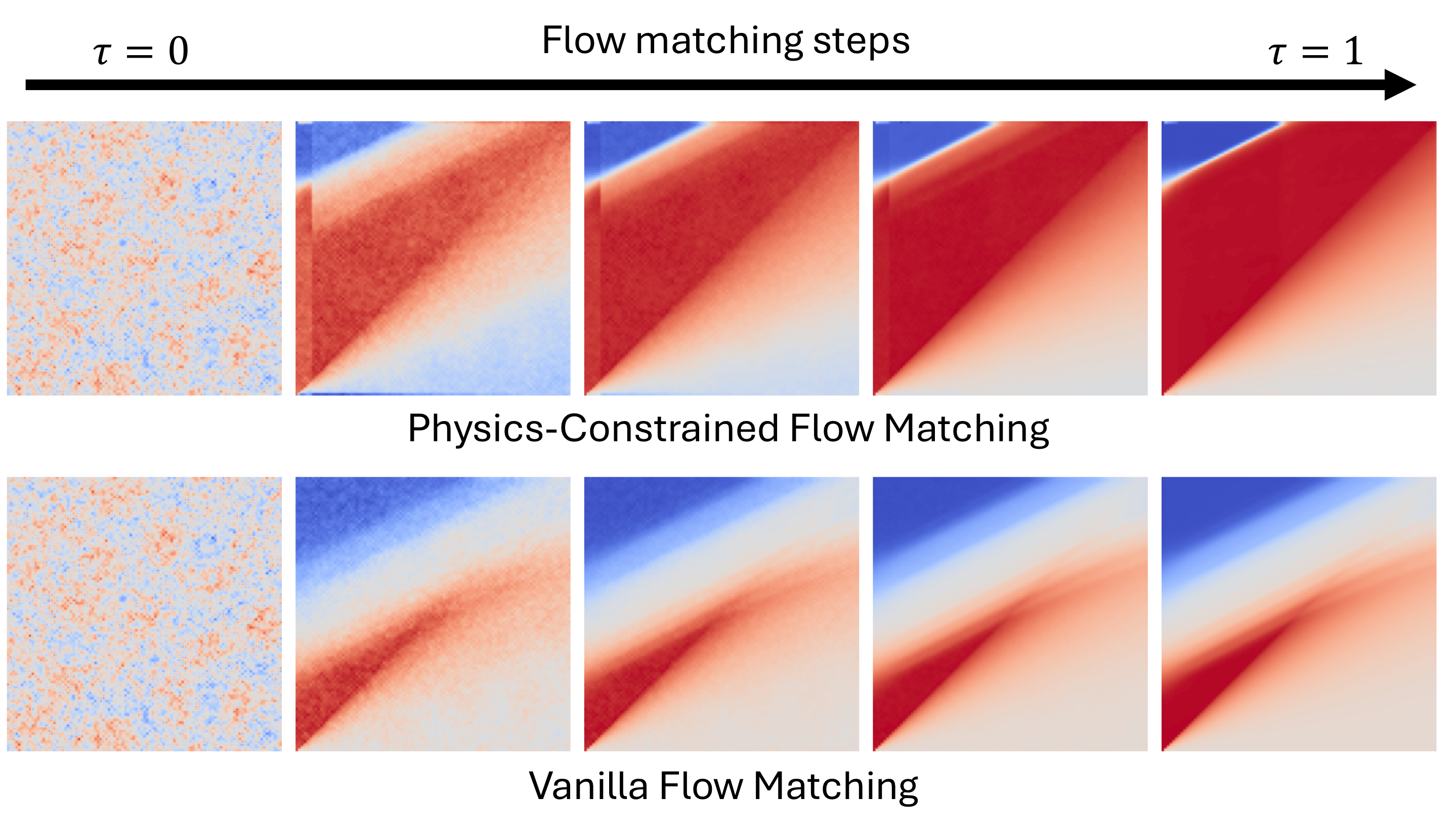
Using a pretrained flow-based model, Physics-Constrained Flow Matching enforces hard physical constraints, such as mass conservations and nonlinear boundary constraints, in the generated solutions during sampling (without retraining the model).

TLDR

• PCFM allows us to enforce constraints during sampling of flow matching models: no retraining, no architecture changes, and not soft penalties.
• It enforces hard physical constraints (initial conditions, Dirichlet and Neumann boundary conditions, global conservation laws, nonlinear residuals, local flux constraints) up to numerical precision.
• On challenging PDEs where constraints are nonlinear or where we stack multiple constraints (i.e. in reaction-diffusion, Burgers with shocks), PCFM achieves constraints satisfaction while improving / maintaining performance (MMSE, SMSE) compared to other methods.

Abstract

Deep generative models have recently been applied to physical systems governed by partial differential equations (PDEs), offering scalable simulation and uncertainty-aware inference. However, enforcing physical constraints, such as conservation laws (linear and nonlinear) and physical consistencies, remains challenging. Existing methods often rely on soft penalties or architectural biases that fail to guarantee hard constraints. In this work, we propose Physics-Constrained Flow Matching (PCFM), a zero-shot inference framework that enforces arbitrary nonlinear constraints in pretrained flow-based generative models. PCFM continuously guides the sampling process through physics-based corrections applied to intermediate solution states, while remaining aligned with the learned flow and satisfying physical constraints. Empirically, PCFM outperforms both unconstrained and constrained baselines on a range of PDEs, including those with shocks, discontinuities, and sharp features, while ensuring exact constraint satisfaction at the final solution. Our method provides a flexible framework for enforcing hard constraints in both scientific and general-purpose generative models, especially in applications where constraint satisfaction is essential.

Results

Burgers (fixed IC, shocks)

For the inviscid Burgers equation with fixed initial condition, we enforce a nonlinear conservation law, IC, and local flux collocation constraints. PCFM captures the shock structure, thereby improving performance, while keeping both IC and mass conservation residuals to machine precision.

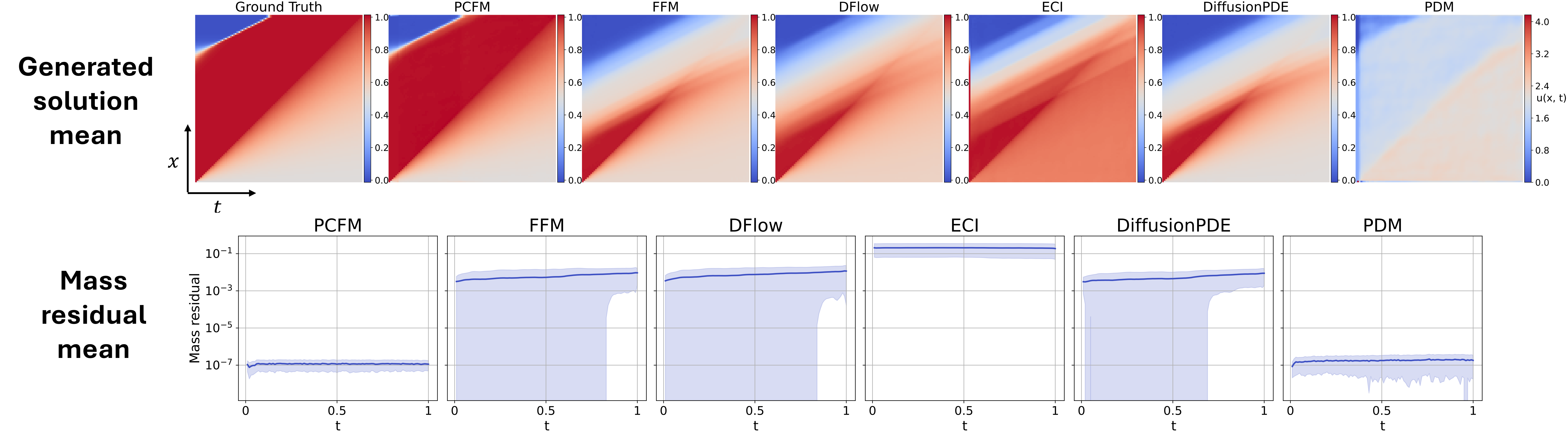
Burgers (Dirichlet + Neumann BCs)

With fixed Dirichlet boundary at the left and Neumann (zero-flux) boundary at the right, we enforce both BCs and nonlinear mass conservation simultaneously. PCFM drives both mass and boundary condition residuals close to machine precision while maintaining competitive MMSE/SMSE and FPD metrics against other methods.

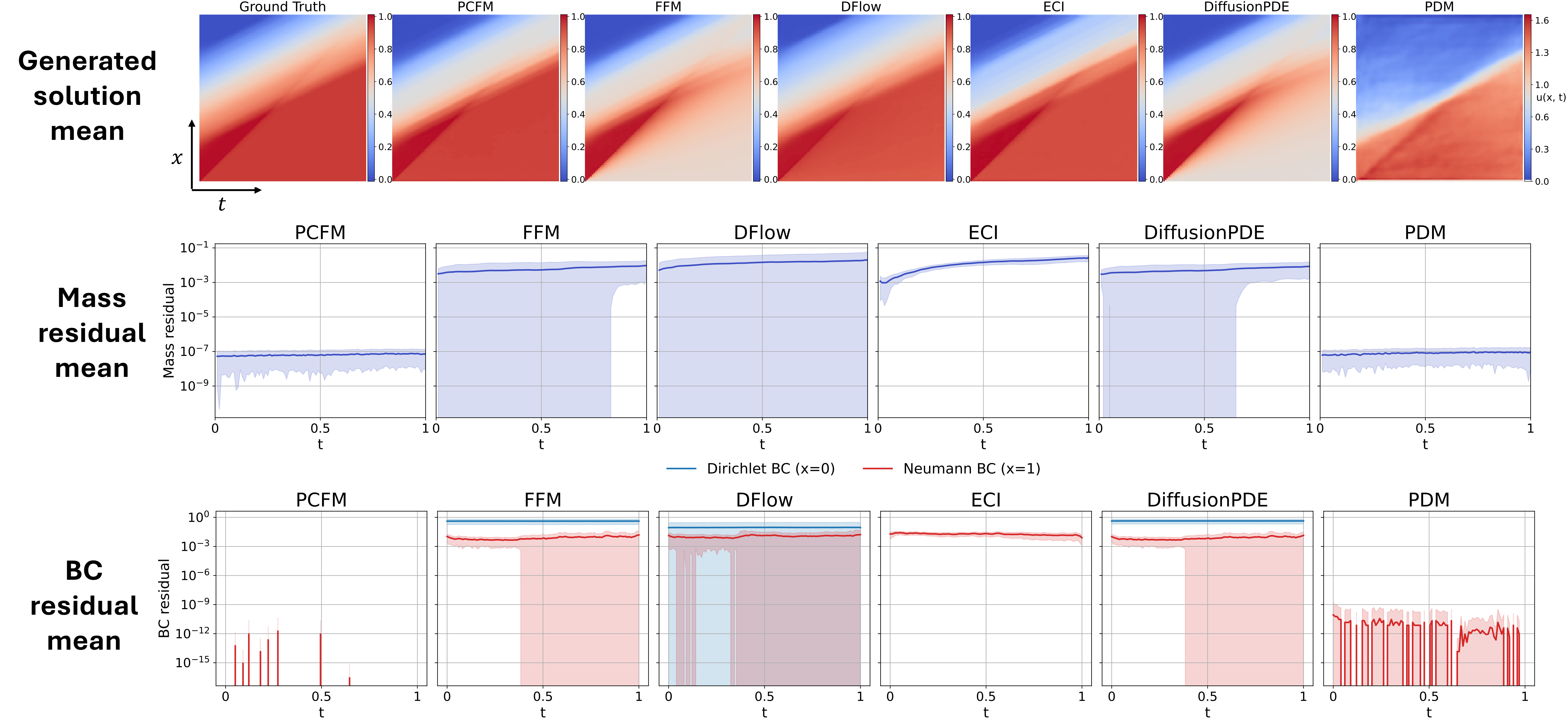
Reaction–Diffusion (nonlinear mass + flux)

For a nonlinear reaction-diffusion equation with Neumann fluxes, the global mass conservation depends on both the nonlinear reaction term and boundary fluxes. PCFM enforces both the fixed IC and this nonlinear mass conservation law, leading to better performance and exactly satisfied constraints to numerical precision. Other methods, including PINN-style losses and updates to the prior noise, all struggle to enforce both constraints or nonlinear constraints.

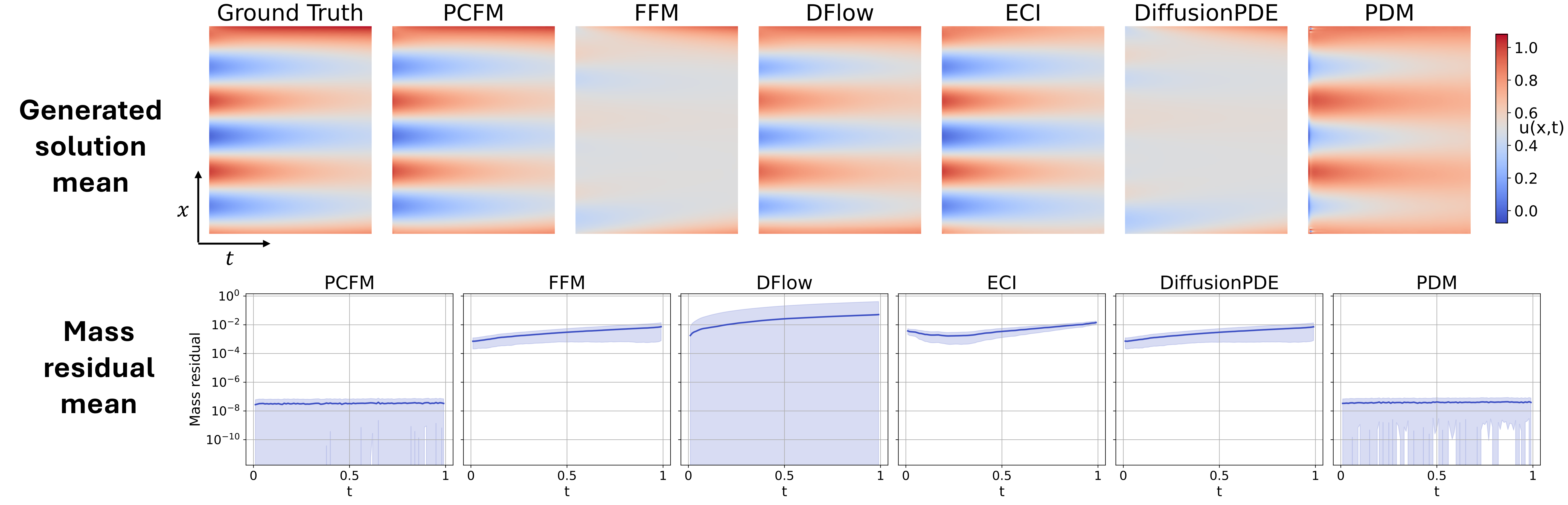
Please refer to our paper for more information on our method and results (including OOD tests)!

Getting started

The easiest way to try PCFM is via the Python implementation: cpfpengfei/pcfm. A Julia implementation is also available at utkarsh530/PCFM.jl. Please feel free to reach out to us for more information on datasets and implementations.

BibTeX

@inproceedings{pcfm2025,
  title     = {Physics-Constrained Flow Matching: Sampling Generative Models with Hard Constraints},
  author    = {Utkarsh and Cai, Pengfei and Edelman, Alan and G{\'o}mez-Bombarelli, Rafael and Rackauckas, Christopher},
  booktitle = {Advances in Neural Information Processing Systems},
  year      = {2025}
}
                    

← Back to home